如何统一计算自己的收益率
目前面临的问题是:投资了太多东西,如货币基金、债券、指数基金等等,但年末缺少统一计算自己当年收益率的方法。经过查阅,常见的收益率计算方法包括简单投资收益率(ROI,Return on Investment)、时间加权收益率(TWR,Time Weighted Retrun)和资金加权收益率(MWR,Money Weighted Return),本文对这三种方法进行介绍,同时用案例说明计算方法,并在最后简述自己的考虑。
收益率计算方法
简单投资收益率 ROI
假设我们的投资场景非常简单,在一开始投入一笔钱,经过一段时间,将本金收益一起取出,则 $$ ROI = \frac{投资净收益}{总投入}\times 100 $$
如果场景复杂化,过程中出现多笔投资,我们计算时可以用累计收益除以投入的本金总和。比如,1 月 1 日投入 10 万,后续再投入 24 万,年底市值 39.6 万元,则到年底累计投入本金 34 万,营利 5.6 万,投资收益率 ROI 为 5.6 / 34 = 16.47%。
ROI 的理解和计算都非常简单,但是它不考虑时间因素造成的影响,在未来投入大量资金会对 ROI 产生很大的影响。例如,假设 1 月 1 日投入 10 万,到 7 月 1 日,总资产增值为 20 万,此时的 R1 = (20-10)/10=100%,即上半年盈利 100%。7 月 1 日再投入 24 万,到 12 月 31 日年底结算,总资产变为 39.6 万,ROI =(39.6-34)/34 = 16.5%,我们得到了“该年收益率为 16.5%”这个结果,但实际上下半年 R2=(39.6-44)/44=-10%,即下半年亏损 10%。
时间加权收益率 TWR
时间加权收益率 TWR 衡量我们的投资在一段时期内的复合收益率。假定投资期限一共分了 n 期,第 i 期的收益率为 Ri(采用 ROI 法进行计算),那么总收益率就是每个时期收益的连乘结果,即
$$ (1+R1)×(1+R2)×…×(1+Rn)\\ = 1 + R $$ 那么最终的业绩回报为:R=(1+R1)×(1+R2)×…×(1+Rn)-1。
假设我们把一年的投资期分为了三段,每一段的收益率分别是-10%、15%和 5%,那么年末的投资收益率 TWR = (1-10%)×(1+15%)×(1+5%)-1 = 8.675%。我们可以看到,在计算 TWR 时,收益率的顺序是无关紧要的,因此它不受外部现金流时间的影响,这使得这种方法极为适合评估一支基金的表现,因为基金经理无法控制每天交易的现金流规模或时间,因此,时间加权收益率 TWR 又称为基金净值法,分段收益率的体现就是基金的净值。
| 日期 | 总资产 | 总份额 | 净值 | 资金 |
|---|---|---|---|---|
| 1 月 1 日 | 10 万 | 10 万 | 1 | |
| 7 月 1 日 | 20 万 | 10 万 | 2 | 流入 24 万 |
| 7 月 2 日 | 44 万 | 22 万 | 2 | |
| 12 月 31 日 | 39.6 万 | 22 万 | 1.8 |
我们仍以简单投资收益率 ROI 一节末尾的例子做一个计算的说明,资金变动如上表所示,假设 1 月 1 日投入 10 万,份额为 10 万份,净值为 1。到 7 月 1 日,总资产增值为 20 万,净值变化为(20 万/10 万份)=2,R1=(20-10)/10=100%,即上半年盈利 100%。
7 月 1 日再投入 24 万,则 7 月 2 日期初,购入份额为(24/2)=12 万份,总资产变为(20+24)=44 万,总份额=10+24/2=22 万份。12 月 31 日年底结算,总资产变为 39.6 万,净值变化为(39.6/22)=1.8。R2=(39.6-44)/44=-10%,即下半年亏损 10%。
综上,时间加权收益率 R=(1+100%)×(1-10%)-1 = 80%,赚了 80%,因为年初净值为 1,所以我们直接看年末净值 1.8 也可以得到“赚了 80%”这个结果。但如果按累计收益法,本金 34 万,期末净资产为 39.6 万,只赚了(39.6-34)/34 = 16.5%。
下面对时间加权法的具体步骤进行总结:
把我们的投资账户理解成小型“私人基金”,将投入的每元钱按 1:1 拆分成“基金份额”;
每日收盘后,用总资产除以基金份额,得到每日的“基金净值”;
取出或投入资金时,该笔资金/当日基金净值,既可得到需相应增减的“基金份额”;
账户日内交易不影响统计,每日刷新收盘的总资产既可,而且对我们个人来说,也不必刻意每日统计,可调整为周/月,在资金进出的当日调整一下“基金份额”既可。
资金加权收益率 MWR
时间加权收益率不受外部现金流时间的影响,资金加权收益率则把外部现金流的大小和流入时间都考虑在内。
如果不考虑资金的投入和取出,期末的总资产 Ve 就等于期初的总资产 Vs 乘以(1+R),R 为收益率 $$ Ve = Vs \times (1 + R) $$ 如果考虑外部现金流的影响,上述公式变为 $$ Ve = Vs \times (1+R)+C \times (1+R) ^{0.5} $$ 该公式简单的理解就是期初投入的资金权重记为 1,其中投入的资金(即外部现金流 C)权重记为 0.5,并与期初资产一样按照收益率 R 产生收益,达到期末资产 Ve,该方法就叫简单内部收益率(Simple Internal Rate of Return)
简单内部收益率公式为超越函数,需要通过数值法迭代计算,手工计算较为复杂。考虑到该公式的一个隐含的含义为“复利”,因此若假设为“单利”,则上述公式可以进行简化,演算过程为 $$ Ve = Vs \ast (1+R)+C \ast (1+R)^{0.5} \\ \approx Vs \ast (1+R)+C\ast(1+\frac{R}{2}) \\ = Vs+C+R\ast(Vs+\frac{C}{2}) $$ 因此,最后结果为 $$ R = \frac{Ve-Vs-C}{Vs+\frac{C}{2}} $$ 我们可以将分子理解为投资收益,将分母理解为等效投资成本,这种方法因为对过程进行了简化,叫做简单 Dietz 方法(Simple Dietz Method),还是以之前的例子来解释,期初资金 Vs = 10 万,年中又投入 24 万,期末资金 Ve=39.6 万,则收益率计算如下 $$ R = \frac{39.6-10-24}{10+\frac{24}{2}} = \frac{5.6}{22} = 25.45% $$
| 日期 | 总资产 | 总份额 | 净值 | 资金 |
|---|---|---|---|---|
| 1 月 1 日 | 10 万 | 10 万 | 1 | |
| 7 月 1 日 | 20 万 | 10 万 | 2 | 流入 24 万 |
| 7 月 2 日 | 44 万 | 22 万 | 2 | |
| 12 月 31 日 | 39.6 万 | 22 万 | 1.8 |
简单内部收益率假设外部现金流权重为 0.5,即假定在区间中点投入,如果投入的时间不是正好在中间,根据简单内部收益率,假定每次的现金流均以收益率 R 产生收益,则收益率公式变为: $$ Ve=Vs\ast(1+R)+\sum_{t=T}^{t=1}C_t\ast(1+R)^{w_t} $$ 其中, $$ W_t = \frac{TD-D_t}{TD} $$ $C_t$为每次的外部现金流,TD 为整个计算周期的天数,$D_t$为期初到发生现金流的天数(包括非交易日)
为了方便计算,上述公式同样可以进行演化,过程如下 $$ Ve=Vs\ast(1+R)+\sum_{t=T}^{t=1}C_t\ast(1+R)^{w_t} \\ \approx Vs\ast(1+R)+\sum C_t\ast(1+W_t\ast R) \\ =Vs+\sum C_t + R\ast(Vs+\sum C_t\ast W_t) $$ 因此,最后结果为 $$ R=\frac{Ve-Vs-C}{Vs+\sum C_t \ast W_t} $$ 叫做修正 Dietz 方法(Modified Dietz Method), 重复上面的案例,区别是 24 万分 2 次投入,期初资金 Vs = 10 万,年中陆续又投入 24 万,其中 4 月流入的 12 万权重为(12-3)/12=3/4,7 月流入的 12 万权重为(12-6)/12= 1/2,(期末资金 Ve=43.2 万,则收益率计算如下 $$ R=\frac{43.2-10-24}{10+12\ast3/4+12\ast1/2} = 36.8% $$
| 日期 | 总资产 | 总份额 | 净值 | 资金 |
|---|---|---|---|---|
| 1 月 1 日 | 10 万 | 10 万 | 1 | |
| 4 月 1 日 | 15 万 | 10 万 | 1.5 | 流入 12 万 |
| 4 月 2 日 | 27 万 | 18 万 | 1.5 | |
| 7 月 1 日 | 36 万 | 18 万 | 2 | 流入 12 万 |
| 7 月 2 日 | 48 万 | 24 万 | 2 | |
| 12 月 31 日 | 43.2 万 | 24 万 | 1.8 |
如果投资期内本金变动频繁,自己又关心长期年复合收益率,可以使用资金加权收益率 MWR 法。
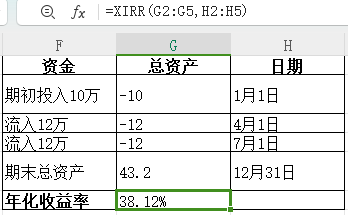
XIRR 内部收益率
MWR 实际上是比较适合我们使用的,但计算起来比较麻烦,Excle 提供的 XIRR 函数是一个比较不错的替代方法,和资金加权收益率的修正 Dietz 方法计算结果可以趋同。
要理解 XIRR,先要理解 IRR 的定义。已知投资期内所有现金流,假设所有的这些现金流具有相同的复合年化收益率,最后得到了我们在期末看到的总资产的值,内部收益率(IRR)就是要算出这个复合年化收益率的值是多少。 而 XIRR 与 IRR 的区别是,IRR 法默认提供给它的每期现金流是”等时间间隔“的,而 XIRR 把每期投入的现金流动首先按投入日期与第一期的日期天数差,折算到”等时间间隔为 1 天“,然后再进一步折算到”年化收益率“。所以,XIRR 法计算出的直接就是年化收益率了,不过要注意函数 XIRR 要求至少有一个正现金流和一个负现金流,且如果一个值是成本或支付,则它必须是负值。
仍以之前的例子说明,1 月 1 日开始,中间有两笔现金流,通过 XIRR 函数,我们得到了年化收益率为 38.12%,与修正 Dietz 方法结果基本相似。
接下来我们做个简单的比较说明
- IRR 算出来的是每期收益率(资金定期流入,资金方向变动 1 次),如月收益率、季度收益率、年收益率等。
- XIRR 算出来的是年化收益率(资金不定期流入流出,资金方向变动 N 次)
- Modified Dietz 算出来的是某个时间段的收益率(不一定是整年)
计算方法选择
两种考虑
一种是把把自己所有的流动性资产,即股票、债券、存款、现金等全部统计进来,这样得到的结果是反映的是自身总资产的升值速度。另一种是只考虑自己的投资资产,即基金和股票账户,反映的是自己的投资能力。
目前计划综合采用时间加权收益率(基金净值)法和 XIRR 内部收益率法,两者比对着来看自己的收益率。其中基金净值法要求每个月末记录账户的资产值。
投资目标
假设未来三十年内通货膨胀率为 3%,M2 货币的年增长率为 7%。如果投资在此期间保持大于 3%的投资收益,那么购买力不会受到损失;如果保持大于 7%的投资收益,那么在社会上的财富地位得以保持。 同理,既然是做稳健投资,长线来看首先要跑赢存款利率,不如直接存银行定期。
参考资料
[1] 投资太多东西,如何统一计算自己的收益率? - 知乎 (zhihu.com)
[2] KlipC 讲解投资收益率、时间加权收益率、资金加权收益率 Part 1 -雪球 (xueqiu.com)
 支付宝
支付宝 微信
微信