计算机基础-实数在计算机中的存储
最近在智能合约中实现信誉算法,但是 Solidity 不支持浮点数赋值和运算,好在有人写了一个库实现了 IEEE 754 浮点数标准,只不过输入输出都是二进制,所以回过头来仔细理解一下实数在计算机中的存储。
1. 实数
实数就是带有整数部分和小数部分的数字。
2. 实数的定点表示
定点表示就是固定小数点的表示法,比如 23.75,就可以表示为 $(10111.11)_2$ $$ 23.75 = 23 + 0.75 = (2^4 + 2^2 + 2^1 + 2^0) + (2^{-1} + 2^{-2}) $$ 但是,由于不确定整数部分和小数部分各需要多少位来存储,很容易出现精度的丢失。
- 小数部分精度受损:用 16 位二进制数表示一个实数,其中整数部分 14 位,小数部分 2 位,此时存储十进制数 1.00234 就会损失精度,最终存储在计算机中的结果是 1.00
- 整数部分精度受损:用 16 位二进制数表示一个实数,其中整数部分 2 位,小数部分 14 位,此时存储十进制数 10.00234 就会损失精度,最终存储在计算机中的结果是 2.00234
因此,为了维持精度,在计算机中存储实数通常采用的是浮点表示法。
3. 实数的浮点表示
浮点的意思是允许小数点浮动,比如,当我们表示十进制数 7500.24 时,采用科学计数法可以将小数点左移 3 位,从而表示为 $7.50024 \times 10^3$,写作 +7.50024E3。通过这种方式我们就可以控制小数点左右任一部分的数字个数,从而便于存储,一般情况我们会在小数点左边仅保留 1 位。
3.1 规范化
科学计数法用于十进制数,当这种小数点浮动的方法用于二进制数时,就叫做浮点表示法。
以上面的数字 23.75 为例,其二进制表示为 $(10111.11)_2$,采用浮点表示法,可以表示为 $1.011111 \times 2^4$。我们通常将这样一个数字划分为三部分:符号 Sign,指数 Exponent 和 尾数 Mantissa。
| |
符号位用一个二进制位表示,0 表示正,1 表示负;尾数指的是小数点右侧的二进制数,定义了该数的精度,小数点和小数点左侧的 1 没有存储,它们是隐含的;指数是小数点移动的位数,使用余码表示法存储,下面进行介绍。
余码表示法的出现是因为指数也有符号,比如 $(10111.11)_2$ 的浮点表示为 $1.011111 \times 2^4$,此时指数为正整数 4,但是$(0.00101)_2$ 的浮点表示为 $1.01 \times 2^{-3}$,此时指数为负整数 -3。如果不想在指数部分使用一个额外的符号位,就要想一种别的表示法,这就是余码表示法。下面我们通过一个例子来介绍它。
4 位的二进制数可以表示 16 个整数,即 -7 到 8,我们采用对它们统一加一个偏移量的方法来把这些数字全部变成非负整数,这个例子中,我们对所有的数字统一 +7,这样十六个整数就变成了 0 到 15,如下图
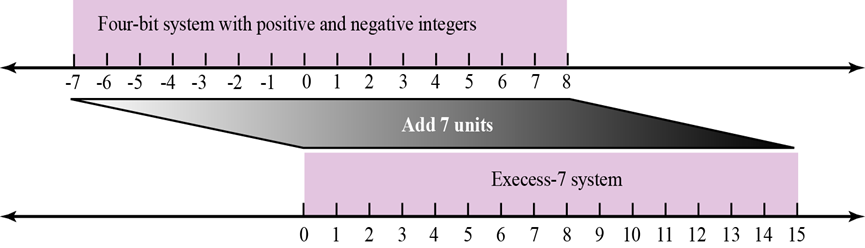
这种加一个偏移量的方法并没有改变数字之间的相对位置,因此当我们得到这样一个数字,又知道了它的偏移量,是可以转换回原本的数字的,这种方法就叫做余码表示法。上例中,偏移量为 7,所以更具体一点可以称为余7码。
3.2 IEEE 754标准
IEEE 制定的 754 标准是关于计算机软硬件浮点数表示和运算的标准,被各大硬件厂商和编程语言所采用。该标准的内容其实就是浮点表示法的三部分各占多少位,如下表
| 单精度(Single Precision) | 双精度(Double Precision) | 四精度(Quadruple Precision) | |
|---|---|---|---|
| 数字位数 | 32 | 64 | 128 |
| 符号位数 | 1 | 1 | 1 |
| 指数位数 | 8 | 11 | 15 |
| 尾数位数 | 23 | 52 | 112 |
| 偏移量 | 127 | 1023 | 16383 |
- 精度:当用 32 位二进制数表示时,我们称为单精度,当用 64 位表示时,我们称为双精度。
- 偏移量:偏移量的计算方法为 $2^{m-1}-1$,$m$ 是指数位数。偏移量是多少,就是余多少码,比如,单精度偏移量为 127,就是余127码。
一个实数转换为浮点数表示的步骤为
- 确定符号位 S;
- 将数的绝对值转换为二进制数;
- 规范化二进制数;
- 确定指数 E 和尾数 M,尾数不足在右侧补0;
- 将 SEM 相连。
下面用一些例子来说明该过程,以及给定一个浮点数的二进制表示表示如何反向计算出这个实数。
Example 1:写出十进制数 -0.0234375 的余127码(单精度)表示法
S = 1(符号位为负)
十进制转换二进制:$0.0234375 = (0.0000011)_2$
规范化:$(0.0000011)_2 = (1.1)_2 \times 2^{-6}$
指数 $E = -6 + 127 = 121 = (01111001)_2$,尾数 $M = (1)_2$
连接 SEM:$(10111100110000000000000000000000)_2$
1 21 01111001 10000000000000000000000 S E M
Example 2:位模式 $(11001010000000000111000100001111)_2$ 以余127码格式存储于内存中. 求该数字十进制计数法的值.
拆分:首位 S,接下来 8 位为 E,剩下的 23 位为 M
1 21 10010100 00000000111000100001111 S E M符号为负号
指数 = E - 127 = 148 - 127 = 21
将 $(1.00000000111000100001111)_2 \times 2^{21}$ 去规范化得到 $(1000000001110001000011.11)_2$
得到的二进制数化为十进制为 2104378.75
最终的数字为 -2104378.75
Example 3:实数 0.0 的存储,这是特例,规定这种情况符号、指数和尾数都为0
后记:所找的的库实现 IEEE 754 标准时,输入输出都是二进制,因此,还需要自行实现两个算法从而实现和十进制实数的相互转换,算法就是上面两个例子的步骤。
 支付宝
支付宝 微信
微信