警告
本文最后更新于 2020-07-11,文中内容可能已过时。
并查集是一种特别而实用的结构,主要作用是进行不相交集合的合并和判断两个元素是否在同一集合,时间复杂度为常数级。常见用途包括 Kruskal 算法和求最近公共祖先,本篇文章介绍该数据结构。
并查集的基本操作为3个,包括初始化、查找与合并
1. 初始化
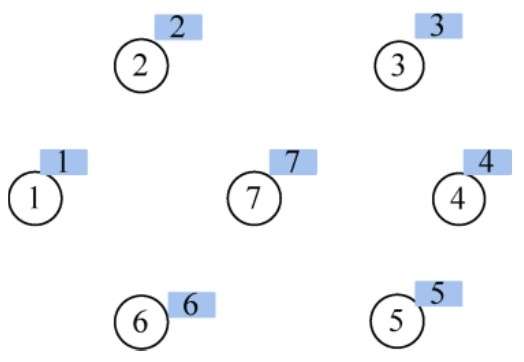
并查集的初始化是将每个元素所作集合初始化为其自身,对数组就是将集合号(元素值)设置为自身编号

1
2
3
4
5
6
| func Init(int n) []int {
father := make([]int,n)
for i := 0; i < n; i++ {
father[i] = i
}
}
|
对链表则是令指针指向自己

2. 查找
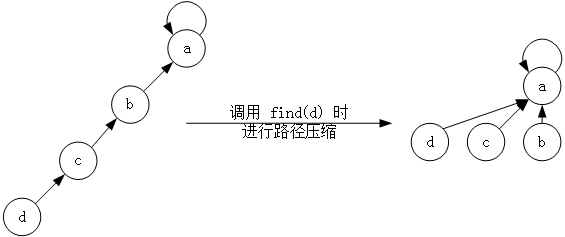
查找就是不断沿着父节点向上,直到根结点,为了将复杂度限制在常数级,可以令查找路径上每个节点都直接指向根结点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| // 递归
func Find(x int) int {
if x != father[x] {
father[x] = Find(father[x])
}
return father[x]
}
// 非递归
func Find(x int) {
p := x
for father[p] != p {
p = father[p]
}
for x != p {
t := father[x]
father[x] = p
x = t
}
return x
}
|
最后的效果如下

3. 合并
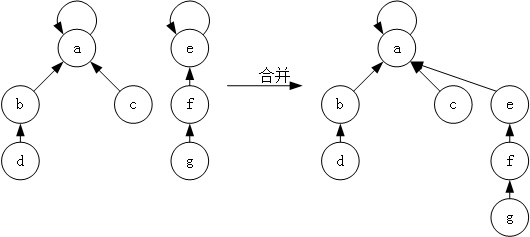
合并的操作也非常简单,就是让一个集合的树根指向另一个集合的树根
1
2
3
4
5
6
7
8
9
10
11
| func Merge(a,b int) int {
p,q := Find(a),Find(b)
if p == q {
return 0
}else if p > q {
father[p] = q
}else{
father[q] = p
}
return 1
}
|
4. 复杂度
如果有n个节点、e条边(关系),每一条边(u, v)进行集合合并时,都要查找u和v的祖宗,查找的路径从当前节点一直到根节点。n个节点组成的树,平均情况下树的高度为logn,因此并查集中,合并集合的时间复杂度为O(elogn)。






 支付宝
支付宝 微信
微信