警告
本文最后更新于 2020-03-28,文中内容可能已过时。
链表是一种最为基础的数据结构,由一系列结点组成,每个结点不仅包含值,还包含指向下一个结点(有时也包括上一个结点)的指针。相比于数组,在链表中访问指定的元素则需要$O(N)$的复杂度,但进行插入和删除操作只需要$O(1)$的复杂度
1. 单链表
一个单链表的例子如下,蓝色箭头显示链表中的结点是如何相连的

关于结点的最常见的定义如下
1
2
3
4
5
| //单链表结点
type node struct {
val int // 结点的值
next *node // 指向下一个结点的指针
}
|
多数情况下,我们使用头结点来表示整个链表,并将链表的长度存储其中。虽然增加了一个结点的存储,但带来的好处却是巨大的
1
2
3
4
5
| //头结点,也是单链表的起始
type singlyLinkedList struct {
length int // 链表长度
next *node // 指向第一个结点的指针
}
|
定义了头结点的情况下,需要事先对链表进行初始化
1
2
3
4
5
6
7
8
| /* @description: 初始化链表(头结点)
@author: shuzang 2020-03-28
@param: 无
@return: _ *singleLinkedList 指向单链表(头结点)的指针
*/
func constructor() *singlyLinkedList {
return &singlyLinkedList{0, nil}
}
|
1.1 获取指定结点的值
本质是对链表的遍历,修改操作也是相同的算法,只是需要遍历到指定元素后进行修改即可,程序实现如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| /* @description: 如果索引有效,获取链表中第 index 个结点的值
@author: shuzang 2020-03-28
@param: index int 要获取的元素位置
@return: _ int 获取元素的值; _ error 索引无效时返回错误
*/
func (list *singlyLinkedList) Get(index int) (int, error) {
if index < 1 || index > list.length {
return -1, errors.New("param - index is invalid")
}
cur := list.next
for i := 1; i < index; i++ {
cur = cur.next
}
return cur.val, nil
}
|
1.2 插入结点
如果我们想在 prev 结点后插入新结点,基本操作步骤如下
- 初始化新结点 newNode
- 将新结点的 Next 指针指向 prev 结点的下一个结点
- 将 prev 结点的 Next 指针指向新结点
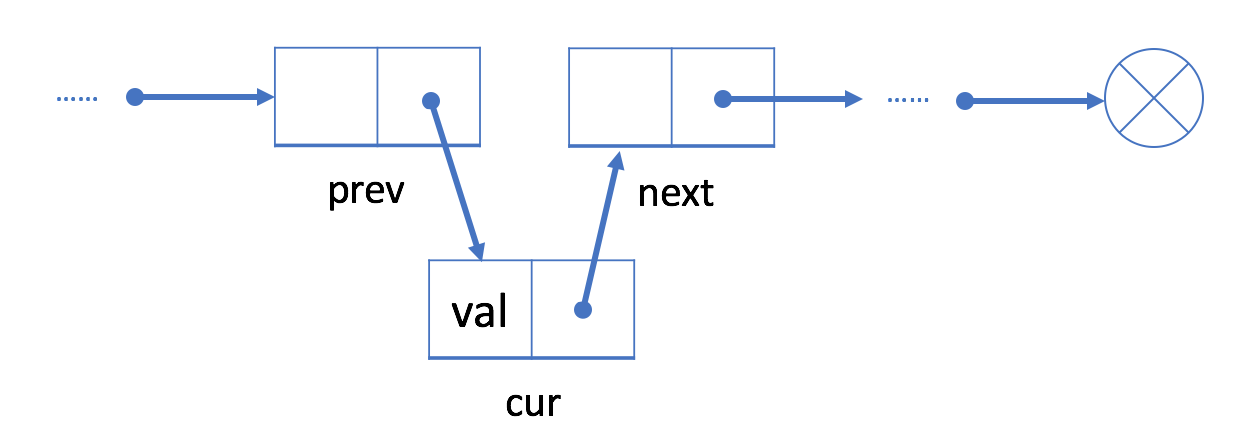
在开头插入结点和在结尾插入结点是两种特殊情况,前者需要考虑头结点的存在,后者需要遍历到链表结尾,我们不再详述。三种插入的程序实现如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| /* @description: 在链表的第一个元素之前插入结点,插入后,新结点将成为链表的第一个结点
@author: shuzang 2020-03-28
@param: val int 要添加的元素的值
@return: 无
*/
func (list *singlyLinkedList) AddAtHead(val int) {
list.next = &node{val, list.next}
list.length++
}
/* @description: 将新结点追加到链表的最后一个元素
@author: shuzang 2020-03-28
@param: val int 要添加的元素的值
@return: 无
*/
func (list *singlyLinkedList) AddAtTail(val int) {
newNode := &node{val, nil}
if list.next == nil {
list.next = newNode
} else {
cur := list.next
for cur.next != nil {
cur = cur.next
}
cur.next = newNode
}
list.length++
}
/* @description: 在链表的第 index 个结点前添加结点,插入后新结点成为第 index 个结点,
如果 index 大于链表长度,结点添加到链表末尾,如果 index 小于 1,则在头部插入结点
@author: shuzang 2020-03-28
@param: index int 要插入的位置,起始数字为 1; val int 要插入的元素的值
@return: 无
*/
func (list *singlyLinkedList) AddAtIndex(index, val int) {
if index > list.length {
list.AddAtTail(val)
} else if index <= 1 {
list.AddAtHead(val)
} else {
cur := list.next
for i := 1; i < index-1; i++ {
cur = cur.next
}
cur.next = &node{val, cur.next}
}
list.length++
}
|
1.3 删除结点
删除结点只需要将前一个结点的 Next 指针指向当前结点的下一个结点,需要注意的是我们只需要遍历到待插入结点的前一个结点即可

程序实现如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| /* @description: 如果索引有效,删除链表第 index 个位置的结点
@author: shuzang 2020-03-28
@param: index int 要删除的元素位置
@return: _ error 索引无效时返回错误
*/
func (list *singlyLinkedList) DeleteAtIndex(index int) error {
if index < 1 || index > list.length {
return errors.New("param - index is invalid")
} else if index == 1 {
list.next = list.next.next
} else {
cur := list.next
for i := 1; i < index-1; i++ {
cur = cur.next
}
cur.next = cur.next.next
}
list.length--
return nil
}
|
1.4 打印链表
一个工具函数,不是必要的,但是很常用,打印输出整个单链表
1
2
3
4
5
6
7
8
9
10
11
12
13
| /* @description: 工具函数,打印单链表
@author: shzuang 2020-03-28
@param: 无
@return: 无
*/
func (list *singlyLinkedList) PrintList() {
cur := list.next
fmt.Println(("当前单链表为: "))
for ; cur.next != nil; cur = cur.next {
fmt.Printf("%v->", cur.val)
}
fmt.Println(cur.val)
}
|
2. 双指针技巧
双指针是一种经典的链表操作技巧,对很多问题都有非常好的作用,下面通过几个经典问题进行介绍
2.1 环形链表
关于环形链表的经典问法是:给定一个链表,判断链表中是否有环。更多扩展的问题包括:
- 如果存在环,找出环的入口结点
- 如果存在环,求环中的结点个数
- 如果存在环,求链表长度
这些问题都可以通过Floyd判环算法解决,算法的基本思想可以拿跑圈来举例说明:假设两个人在一条环形跑道上跑步,同时出发,但速度一个快一个慢,我们知道,如果一直跑下去,快的人总能追上慢的一方,此时快的一方多跑的路程一定是跑道长度的整数倍,即我们所说的「套圈了」
有人也拿龟兔赛跑举例,但思想是相同的。基于上述思想,Floyd提出了双指针算法(快指针和慢指针),算法分两个阶段。
第一阶段可以用来判断是否有环。慢指针(龟)每次前进一步,快指针(兔)每次前进两步(两步或多步效果是等价的,只要一个比另一个快就行)。如果两者在链表头以外的某一点相遇(即相等)了,那么说明链表有环,否则,如果(快指针)到达了链表的结尾,那么说明没环。

第二阶段确定环的起点。假设链表起点到环的起点距离为$F$(这里我们提到的距离是结点个数),第一阶段相遇时的结点距离环的起点为$a$,环的周长为 $n = a + b$。那么第一阶段两者相遇时,慢指针移动的总距离为 $d = F + r_1 n + a$,由于快指针移动速度是慢指针的两倍,其移动的总距离为$2d = F + r_2 n + a$,其中$r_1$为慢指针第一次相遇时转过的圈数,$r_2$为快指针第一次相遇时转过的圈数。我们令两者相减(快减慢),那么得到 $d = (r_2 - r_1)n$,意为 $d$ 是环长度的倍数。
因此,我们将慢指针移动到链表的起点,快指针保持在第一次相遇的结点,然后两者同时开始移动,但这次两者每次都只移动一步。当慢指针前进了 $F$ 到达环的起点时,快指针距离链表起点 $d + F$,由于 $d$ 是环长度的倍数,这个距离可以看作快指针从链表起点出发,走到环的起点,然后绕环转了几圈,但此时停在了环的起点。即两个第二次的相遇点就是环的起点。
程序实现如下,需要注意的有两点
- 调用 Next 字段前,检查结点是否为空
- 仔细考虑循环的结束条件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| func detectCycle(head *LinkedList) *Node {
slow, fast := head.Next,head.Next
//第一阶段,循环退出条件为fast指针或fast.Next为nil,因为fast始终在slow前面,所以不需要判断slow
for fast != nil && fast.Next != nil {
slow = slow.Next
fast = fast.Next.Next
if fast == slow {
slow = head
break
}
}
//退出循环要么是到达相遇点,要么是没有环,没有环时返回nil
if fast == nil || fast.Next == nil {
return nil
}
//第二阶段,每次移动一步直到相遇,slow指针已经调整完毕
for fast != slow {
slow = slow.Next
fast = fast.Next
}
return fast //此时fast == slow,返回任一个都可以
}
|
得到环的起点后,快指针再跑一圈就可以得到环的长度,相应的,慢指针移回链表起点再走一遍然后和环的长度相加可以得到链表长度。
2.2 相交链表
经典问法是:判断两个无环链表是否相交,如果相交,求相交的起始结点。如下图在 c1 结点相交。

基本求解步骤如下
- 创建两个指针 pA 和 pB,分别初始化为链表
A 和 B 的头结点。然后让它们向后逐结点遍历。 - 当 pA 到达链表的尾部时,将它重定位到链表 B 的头结点 (注意,是链表 B);类似的,当 pB 到达链表的尾部时,将它重定位到链表 A 的头结点。
- 若在某一时刻 pA 和 pB 相遇,则该结点为相交结点。
可以这样理解,除去相交部分(3个结点),A 有 2 个结点,B有 3 个结点。重定位后,A多走的距离正好是重定位前少走的距离,这样直到相交,两者都走了 2+3+3 个结点距离。
程序实现如下,正常情况两个链表不相交的条件是最后一个结点不相同,但是实际上如果任意一个链表为空或两者不相交,根据循环最后都会走到 nil,因此也会跳出循环,而且返回pA或pB的值 nil 也是我们想要的返回值,如果相交,同样直接返回pA或pB的值即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| func getIntersectionNode(headA, headB *LinkedList) *Node {
pA,pB := headA.Next, headB.Next
for pA != pB {
if pA == nil {
pA = headB.Next
}else{
pA = pA.Next
}
if pB == nil {
pB = headA.Next
}else{
pB = pB.Next
}
}
return pA
}
|
其它资料
Leetcode刷题总结之链表





 支付宝
支付宝 微信
微信