算法-递归

首先简单阐述一下递归、分治、动态规划和贪心这几个东西的区别和联系。

1. 递归是一种编程技巧，一种解决问题的思维方式；
2. 分治和动态规划是建立在递归基础上的，解决更具体问题的两类算法思想（实现动态规划大都不是递归的，但是过程和思想是）；
3. 贪心是动态规划的一个子集，可以更高效解决一部分更特殊的问题。

1. 递归原理

递归的基本思想是某个函数直接或者间接地调用自身，核心在于将原问题拆解为性质相同但规模更小的子问题，函数不断地调用自身来解决子问题，直到分无可分，也就是到了无需递归就可以解决的地步，原问题就顺利解决掉了。

因此我们在思考递归问题时应明确两点

1. 明确递推关系，也就是原问题如何拆分到更小的子问题
2. 明确结束条件，也就是最小的问题如何不使用递归来解决

我们将递归的基本思路概述为一个模板如下

1
2
3
4
5
6

func Recursive(传入数值) {
  if 结束条件 
      return 最小子问题解
  Recursive(缩小规模)
  利用递归结果进行计算[可选]
}

下面以一个简单的问题「以相反的顺序打印字符串」来进行说明。我们将函数定义为 printReverse(str[0…n-1])，其中str[0] 表示字符串的第一个字符，然后进行分析

1. 分解子问题。原问题可以拆解为先以相反的顺序打印子字符串 str[1…n-1]，然后打印第一个字符 str[0]
2. 结束条件。结束条件为如果当前字符串为空，直接返回。

最终得到的代码如下

1
2
3
4
5
6
7

func printReverse(s []byte) {
    if len(s) == 0 {
        return
    }
    printReverse(s[1:])
    fmt.Printf("%c",s[0])
}

需要我们牢记的一个结论是：凡是可计算函数都是一般递归函数，这就是著名的丘奇-图灵论点。

继续以「反转链表」为例进行说明，虽然迭代的方法更优，但这里我们只介绍递归的思路。

1. 结束条件是当前节点为 nil 或者当前节点的下一个节点为 nil，这两种情况不需要反转
2. 子问题就是反转当前节点后面的部分
3. 递归后要做的事情就是如何将当前节点添加到后面的反转的链表的末尾

因此最后得到的代码如下

1
2
3
4
5
6
7
8
9

func reverseList(head *ListNode) *ListNode {
    if head == nil || head.Next == nil {
        return head
    }     
    tmp := reverseList(head.Next)
    head.Next.Next = head
    head.Next = nil
    return tmp
}

这里最后的处理过程可以这样理解，假设列表为： $$ n_1 → … → n_{k-1} → n_k → n_{k+1} → … → n_m → Ø $$ 若从节点 $n_{k+1}$ 到 $n_m$ 已经被反转，而我们正处于 $n_k$。 $$ n_1 → … → n_{k-1} → n_k → n_{k+1} ← … ← n_m $$ 我们希望 $n_{k+1}$ 的下一个节点指向 $n_k$, 那么只需要调整 $n_k$ 的指针即可，因为此时后面的链表末尾已经是节点 $n_{k+1}$ 了。所以执行

1
2

nk.Next.Next = nk
nk.Next = nil // 处理边界条件 n1，否则产生循环

还应该明白代码最后返回的 tmp 不是当前处理节点的下一个节点，而是后面已反转链表的头结点，这个头结点的指针是一级一级递归传回来的。

写递归最重要的一点是： 明白一个函数的作用并相信它能完成这个任务，千万不要试图跳进细节。 如果跳进一层又一层的递归函数里思考，就会陷入无穷无尽的细节，人脑不是为了做这个的，递归本身就是在简化思维。比如上面的「反转链表」例子，我们确认了子问题具有与原问题相同的性质，因此 reverseList(head.Next) 可以翻转链表后面的部分，我们需要相信这一点，而不是跟随递归进入一层层的调用栈。

2. 记忆化技术

递归的过程可能出现大量重复的计算，以斐波那契数列为例，如果我们定义函数 F(n) 表示在索引 n 处的斐波那契数，那么你可以推导出如下的递推关系：

1

F(n) = F(n - 1) + F(n - 2)

下面的树显示了在计算 F(4) 时发生的所有重复计算（按颜色分组）。

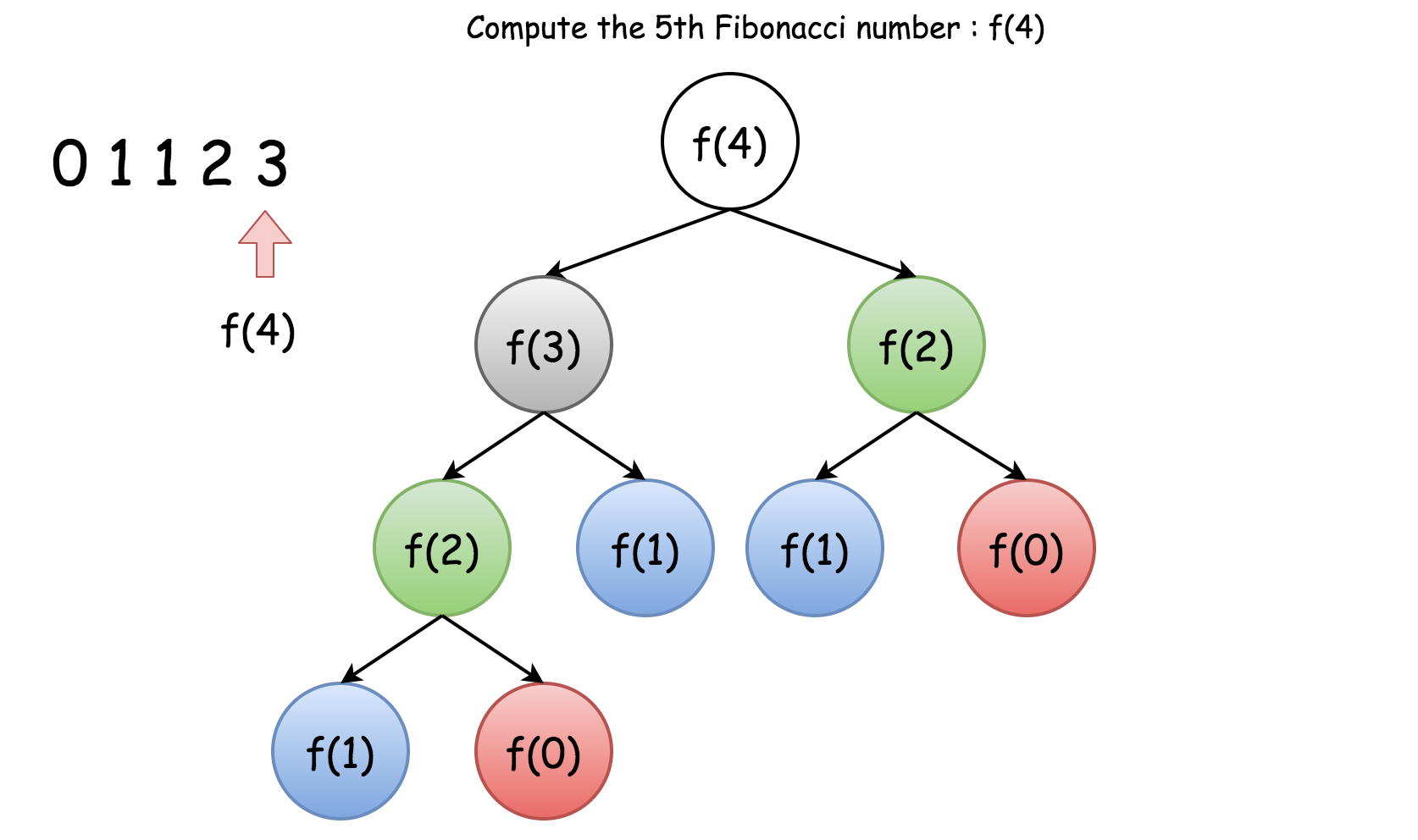
为了消除上述情况中的重复计算，采用的一种方法是将中间结果存储在缓存中，以便随时重用，而不需要重新计算。这种方式叫做记忆化。

记忆化与动态规划的 DP 数组非常相似，但用在递归过程中，一般作为全局变量声明，或者由父函数通过参数进行传递。斐波那契树计算的记忆化方法举例如下

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

var cache = map[int]int{0: 0, 1: 1}

func fib(N int) int {
    if N <= 1 {
        return N
    }
    return memoize(N)
}

func memoize(N int) int {
    if _, ok := cache[N]; ok {
        return cache[N]
    }
    cache[N] = memoize(N-1) + memoize(N-2)
    return memoize(N)
}

3. 复杂度分析

3.1 时间复杂度

给出一个递归算法，其时间复杂度$O(T)$ 通常是递归调用的数量（记作 R） 和计算的时间复杂度的乘积（表示为 $O(s)$）的乘积： $$ O(T) = R * O(s) $$ 以反转字符串为例，由于每次将问题缩减为除第一个字符外的子串，因此函数一共被递归调用 n 次，n 为字符串长度。每次递归调用完毕后，仅仅将第一个字符输出，该操作的时间复杂度为 $O(1)$，因此总体时间复杂度为 $n * O(1) = O(n)$

对于递推关系涉及多个递归调用的情况，比如斐波那契数，其递推关系被定义为 f(n) = f(n-1) + f(n-2)，最好使用执行树来分析时间复杂度。执行树是一棵用于表示递归函数执行流程的树，树中每个节点都表示递归函数的调用，因此树的节点总数就对应递归调用的数量。

递归函数的执行树将形成 n 叉树，其中 n 作为递推关系中出现递归的次数。例如，斐波那契函数的执行将形成二叉树。

如果构成了一棵 n 层的完全二叉树，那么节点总数就是 $2^n - 1$，因此时间复杂度计算中的递归调用数量就是 $O(2^n)$，算上最后的结果处理 $O(1)$，总的时间复杂度为 $O(2^n)$

但是如果我们使用了记忆化技术，从 1 到 n 每个值对应的斐波那契数计算只会发生一次，因此递归调用的数量变为 $O(n)$，最终的时间复杂度为 $O(n) * O(1) = O (n)$

3.2 空间复杂度

空间复杂度考虑两部分：递归相关空间和非递归相关空间。

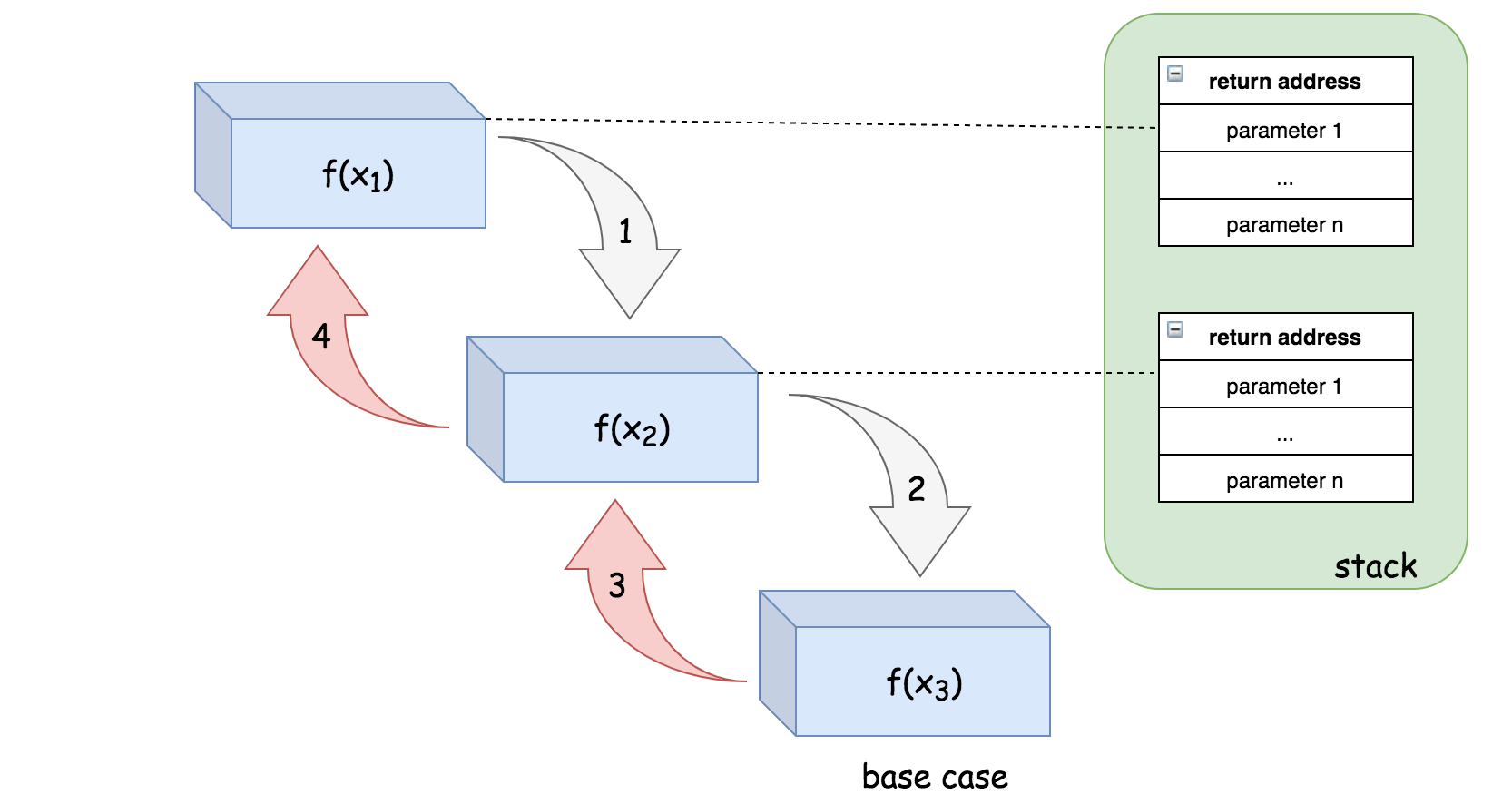
递归相关空间指由递归直接引起的内存开销，即用于跟踪递归函数调用的堆栈，为了完成函数调用，系统会在栈中分配空间来保存三个重要信息

1. 函数调用的返回地址
2. 传递给函数调用的参数
3. 函数调用的局部变量

该空间在函数调用时产生，在调用完成后释放，但对于递归，栈空间将逐渐累积直到结束条件。递归函数中如果没有额外的空间消耗，则递归调用引起的栈空间消耗是递归空间复杂度的主要来源。

仍以反转字符串为例，函数处理逻辑中只有打印首字符会使用常数级空间，递归调用 n 次一共会产生 n 级的栈空间，因此最终的空间复杂度为 $O(n)$。

由于为程序提供的栈空间通常是有限的，在递归调用层级过多时，可能会发生堆栈溢出的情况，此时无法分配新的栈空间进行下一步的递归调用，因此导致程序执行失败。所以在涉及递归算法时，应仔细评估在输入规模扩大时是否存在堆栈溢出的可能性。

非递归相关空间指与递归过程没有直接关系的内存空间，比如上面讨论中提到的打印首字符使用的空间，除此外还可能包括如全局变量等其它的空间使用，比如在利用记忆化优化递归时使用的全局数组，会占用 O(n) 的空间复杂度。

注意，这里递归相关空间与非递归相关空间不是相乘的关系。

4. 尾递归

尾递归是递归函数的一种特殊情况，其中递归调用是递归函数的最后一条指令，并且其返回值不是表达式的一部分。举个例子

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

// 非尾递归
func helper(start int, ls []int) int {
    if start >= len(ls) {
        return 0
    }
    return ls[start] + helper(start+1, ls)
}

// 尾递归
func helper(start int, ls []int, acc int) int {
    if start >= len(ls) {
        return acc
    }
    return helper(start+1,ls,acc+ls[start])
}

说的更通俗一点就是，调用语句是函数最后一条语句，且返回值不会被用作其它计算。

尾递归的好处是避免递归调用期间栈空间的累积，因为每一层的返回不做处理直接返回，相当于不需要这一步直接返回元素调用。此时我们无需保存每一层递归的环境，这导致了从最高层级到结束条件我们始终重用一个栈空间。

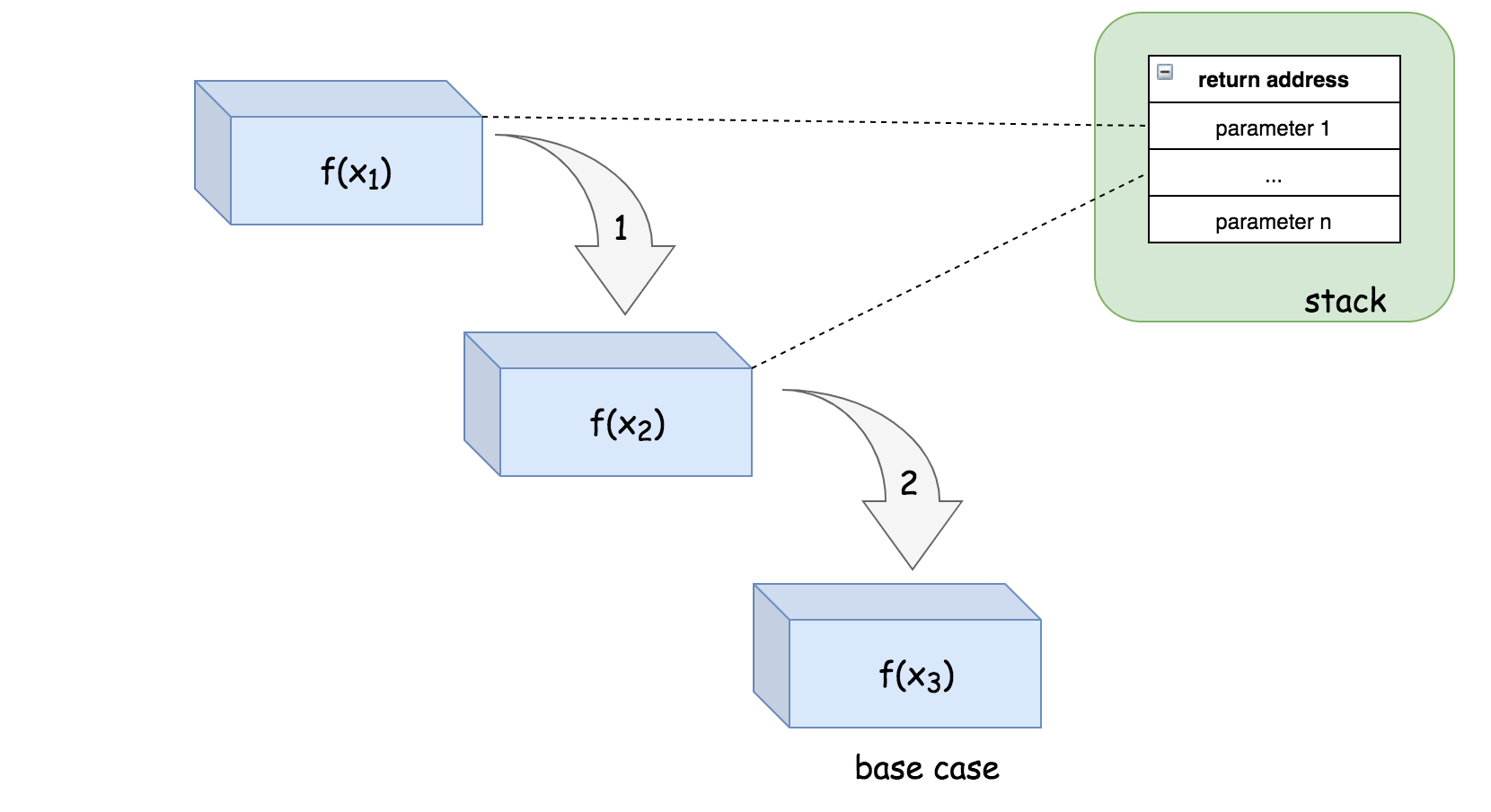
尾递归当然也可以作为非尾递归函数来执行，此时不会重用栈空间，仍然会逐级累积，不过通常编译器会识别尾递归模式进行优化，但这需要编程语言的支持，C、C++支持尾递归优化，Java、Python，我当前使用的 Go 都不支持尾递归优化。

5. 原则

递归的作用非常强大，但可能出现堆栈溢出，因此，可能的情况下，尽量使用记忆化技术节省调用次数，使用尾递归节省栈空间。