警告
本文最后更新于 2020-08-06，文中内容可能已过时。
奇安信的笔试遇到了完全背包问题，结果写的时候按 0-1 背包写的贪心，最后没 AC，因此本篇对所有的背包问题做一次整理。
1. 0-1 背包
问题描述如下
有 n 个物品和一个容量为 W 的背包，每个物品有重量 $w_i$ 和价值 $v_i$ 两种属性，要求选若干物品放入背包使背包中物品的总价值最大且背包中物品的总重量不超过背包的容量。
解决该问题实际上可以用我们学到的所有算法，下面做一点解释
1.1 递归
选择装入背包的物品时，每种物品 $i$ 只有两种选择：装入或不装入。不能将物品 $i$ 装入背包多次，也不能只装入部分物品，我们用 $x_i$ 表示对第 $i$ 个物品的选择，$x_i=1$ 表示选择该物品，$x_i=0$ 表示不选择该物品。这样，对所有的物品，我们就有了一个解集 $(x_1,x_2,……,x_n)$，最终的目标是求得 $max \sum_{i=1}^n v_i x_i$，并且可以将问题写成如下的数学形式
$$
\sum_{i=1}^n w_i x_i \leq c \\
x_i \in \{0,1\}, 1 \leq i \leq n
$$
接下来定义子问题，假设 $m(i,j)$ 代表当前背包剩余容量为 $j$ 时，可选物品为 $i,i+1,…,n$ 时的最大总价值，那么对于第 i 个物品，有两种可能
- 背包剩余容量不足以容纳该物品，此时背包总价值不会变，$m(i,j) = m(i+1,j)$
- 背包剩余容量可以装下该物品，此时如果装物品，总价值会变为 $m(i+1,j-w_i)+v_i$，如果不装该物品，总价值为 $m(i+1,j)$，需要选择两者中总价值更大的那一个
综上我们就得到了递推关系式，然后我们还可以确定边界条件为剩余物品只有一个，也就是 $m(n,j)$，如果能装下第 $n$ 个物品，$m(n,j)=v_n$，否则 $m(n,j)=0$，这样就得到了下面的程序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| package main
import (
"fmt"
)
func main() {
var (
v = []int{12, 10, 20, 15}
w = []int{2, 1, 3, 2}
)
var Knapsack_Recurrence func(i, j int) int
Knapsack_Recurrence = func(i, j int) int {
res := 0
// 边界条件：只有一个物品
if i == len(v)-1 {
if w[i] > j {
res = 0
} else {
res = v[i]
}
} else if w[i] > j {
// 装不下当前物品
res = Knapsack_Recurrence(i+1, j)
} else {
// 可以装下当前物品
t1 := Knapsack_Recurrence(i+1, j)
t2 := Knapsack_Recurrence(i+1, j-w[i]) + v[i]
if t1 > t2 {
res = t1
}else{
res = t2
}
}
return res
}
fmt.Println(Knapsack_Recurrence(0, 5))
}
// Output:
37
|
这里时间复杂度为 $O(2^n)$，空间复杂度为 $O(n)$
1.2 动态规划
动态规划解法与递归法的区别在于使用数组来存储计算的中间值，从而减少重复计算，上面的递推关系式就是现成的状态转移方程。那上面程序中的输入举例，物品数量为 4，背包容量为 5，问题分析和绘制的动态规划数组如下
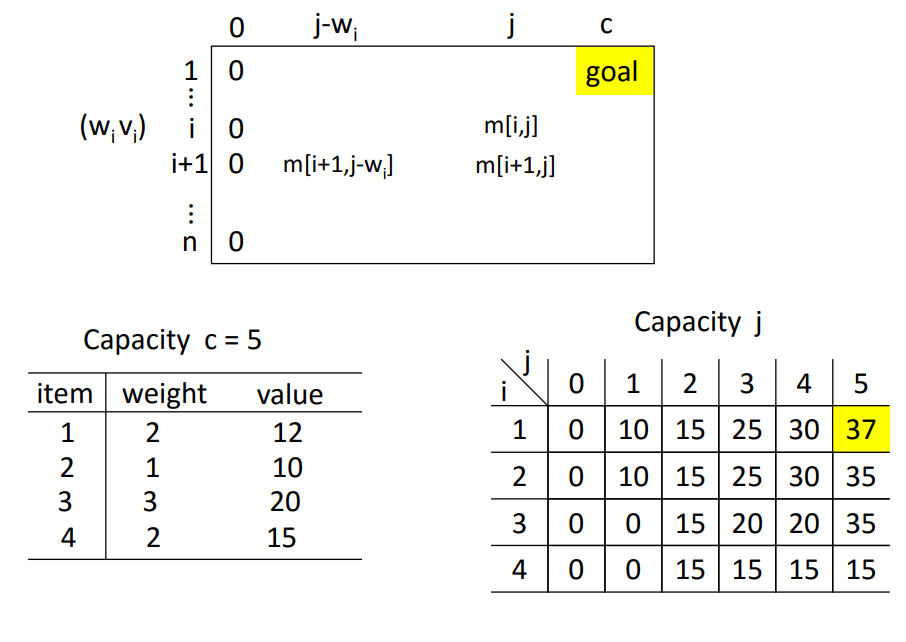编写程序如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| package main
import (
"fmt"
)
var (
v = []int{12, 10, 20, 15}
w = []int{2, 1, 3, 2}
)
func main() {
fmt.Println(Knapsack_dp(4, 5))
}
func Knapsack_dp(N, C int) int {
// 状态数组初始化
dp := make([][]int, N)
for i := 0; i < N; i++ {
dp[i] = make([]int, C+1)
}
// 边界条件
for i, j := N-1, 1; j <= C; j++ {
if w[i] > j {
dp[i][j] = 0
} else {
dp[i][j] = v[i]
}
}
// 填写状态数组, 自底向上，自左到右
for i := N - 2; i >= 0; i-- {
for j := 1; j <= C; j++ {
if w[i] > j {
dp[i][j] = dp[i+1][j]
} else {
dp[i][j] = max(dp[i+1][j], dp[i+1][j-w[i]]+v[i])
}
}
}
return dp[0][C]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
// Output:
37
|
动态规划的时间复杂度为 $O(NC)$，空间复杂度为 $O(NC)$，如果背包容量很大，比如达到了 $2^N$ 基本，性能反而会不如递归方法。
动态规划数组可以进一步优化，主要是因为我们在计算时实际上只用到了前一行的数据，因此二维数组可以简化为一维数组，空间复杂度可以缩减到 $O(C)$
1.3 贪心
贪心解背包问题就是另一种思路了，核心是选择贪心的策略，这里主要使用价值重量比策略。我们可以将过程总结为三步
- 计算每种物品单位重量的价值 $v_i/w_i$，$O(n)$
- 将计算得到的价值重量比按降序排列
- 将尽可能多的单位重量价值最高的物品装入背包，$O(nlogn)$
下面解决的问题实际上是背包的一种情况，即物品装入背包时可以选择背包的一部分，而不是必须全部装入。程序实现如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| package main
import (
"fmt"
"sort"
)
type item [][3]int
func (this item) Len() int {
return len(this)
}
func (this item) Swap(i, j int) {
this[i], this[j] = this[j], this[i]
}
func (this item) Less(i, j int) bool {
return this[j][0] < this[i][0]
}
var (
v = []int{12, 10, 20, 15}
w = []int{2, 1, 3, 2}
)
func main() {
fmt.Println(Knapsack_greedy(4, 5))
}
func Knapsack_greedy(N, C int) int {
res, i := 0, 0
// 计算价值重量比，并存入解数组，解数组每个元素是长度为3的数组
// 其中，第一个为比值，第二个为物品价值，第三个为物品重量
x := make(item, 0)
for i = 0; i < N; i++ {
x = append(x, [3]int{v[i] / w[i], v[i], w[i]})
}
// 对价值重量比进行降序排列
sort.Sort(x)
// 按序装入背包
for i = 0; i < N; i++ {
if x[i][2] > C {
break
}
res += x[i][1]
C -= x[i][2]
}
// 装入第 i 个物品的一部分
if i < N {
res += C * x[i][0]
}
return res
}
// Output:
37
|
时间复杂度为 $O(N)$，空间复杂度为 $O(N)$
1.4 回溯
回溯也是解背包问题的一种方法，可以和递归法进行对比，递归法其实就相当于对解空间树进行了一次搜索，回溯的目的是减小搜索空间。
设物品重量为 $w=[16,15,15]$，物品价值为 $v=[45,25,25]$，背包容量 $c=30$。定义 $r$ 为当前背包的剩余容量，$v$ 为当前背包的价值。因为物品有 3 个，所以树深为 3+1=4，又因为每个解元素有两种取值，1为放入背包，0为不放入，所以每个结点有两棵子树，最终解空间树绘制如下
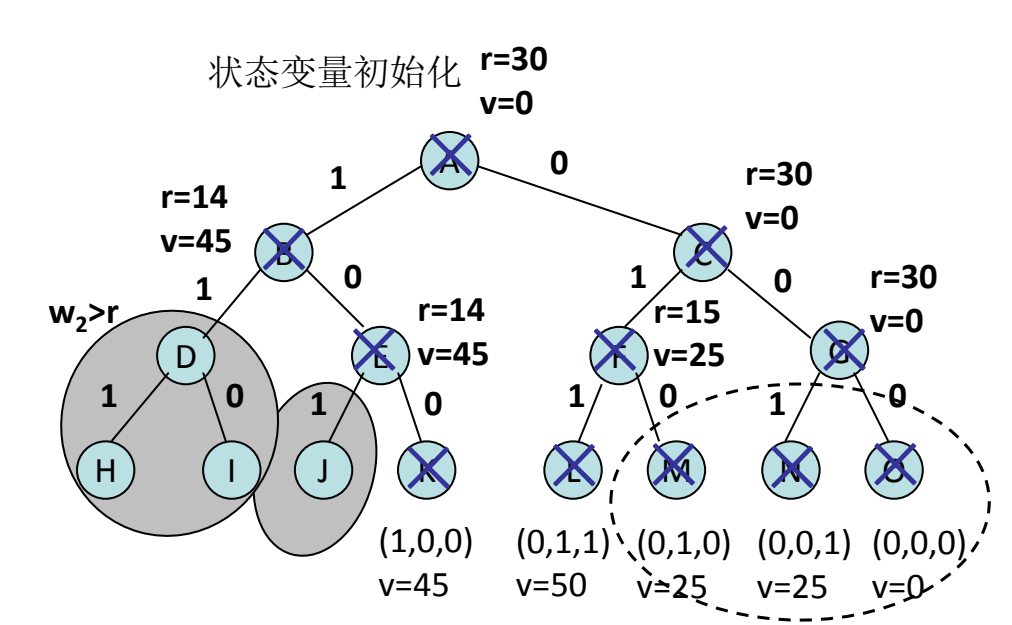
约束和限界函数描述如下
- 约束函数：就是不可行的解，比如上图第二层第一个结点，r=14，小于当前物品重量 15，因此所有子树都不可行；
- 限界函数：就是非最优解，比如上图虚线框起来的结点，因为之前得到的最大价值为 v=50，这里出现的 v 都小于该值，所以不是最优解。右子树价值上界的判断使用的是价值重量比的贪心策略。
算法如下
1.5 分支限界
如果回溯能解，那么分支限界就能解
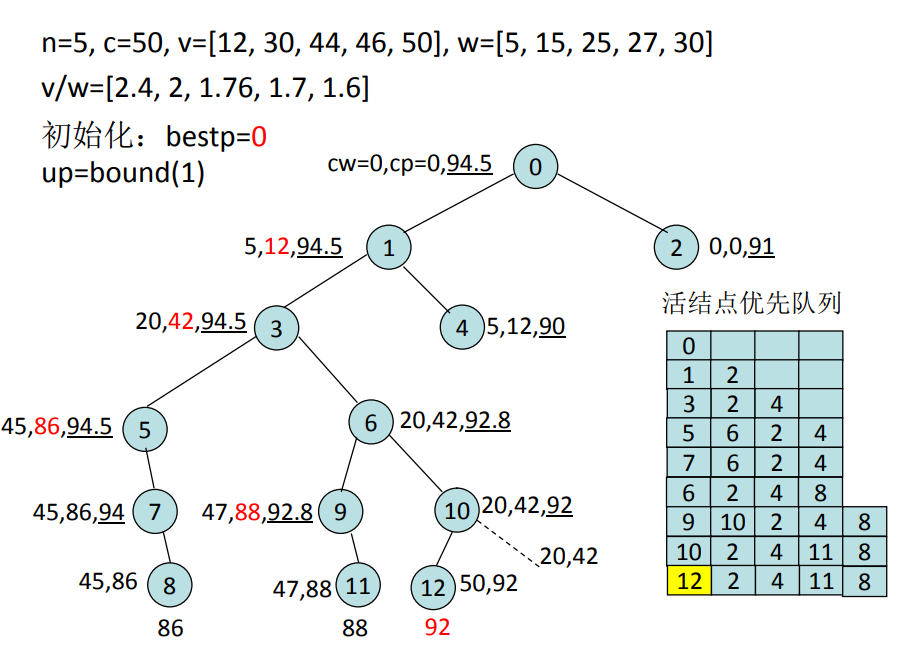
- 首先检查当前扩展结点的左儿子结点(x[i]=1)的可行性。 如果该左儿子结点是可行结点，则将它加入到子集树 和活结点优先队列中。
- 当前扩展结点的右儿子结点(x[i]=0)一定是可行结点，仅 当右儿子结点满足上界约束时才将它加入子集树和活 结点优先队列。
- 节点的优先级由上界函数来决定，即已装袋的物品价值与剩下 的最大单位重量价值的物品装满剩余容量的价值之和。
- 当扩展到活结点优先队列中的叶结点时得到问题的最 优解。
2. 完全背包
完全背包问题相比于01背包的区别就是，只要背包装的下，每个物品可以选任意次，而不是只有一次。
此时解向量的值不再是0或者1，而是有了多种可能，注意的是，这里物品不能只装入一部分，因此贪心算法是不可用的。举个反例也非常简单：假设有两个物品A和B，价值分别为5和8，重量分别为5和7，背包容量为10，物品B的价值重量比显然更高，所以贪心算法会放入一个物品B，此时剩余容量不足以放下 A或者B，得到的总价值为8，但实际上，放入两个 A 可以得到更高的价值10。
我们用动态规划求解，$m(i,j)$ 依然代表当前背包剩余容量为 $j$ 时，可选物品为 $i,i+1,…,n$ 时的最大总价值，对于第 $i$ 中物品，我们有 $k$ 种选择，这样得到状态转移方程
$$
m(i,j) = max{m(i+1,j-w_ik)+v_ik}; 0 \le w_ik \le j
$$
实质就是0-1背包加一层选择物品数量的循环，程序如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| package main
import (
"fmt"
)
var (
v = []int{12, 10, 20, 15}
w = []int{2, 1, 3, 2}
)
func main() {
fmt.Println(Knapsack_dp(4, 5))
}
func Knapsack_dp(N, C int) int {
// 状态数组初始化
dp := make([][]int, N)
for i := 0; i < N; i++ {
dp[i] = make([]int, C+1)
}
for i, j := N-1, 1; j <= C; j++ {
k := 0
for k*w[i] <= j {
k++
}
dp[i][j] = (k - 1) * v[i]
}
// 填写状态数组, 自底向上，自左到右
for i := N - 2; i >= 0; i-- {
for j := 1; j <= C; j++ {
for k := 0; k*w[i] <= j; k++ {
dp[i][j] = max(dp[i+1][j], dp[i+1][j-k*w[i]]+k*v[i])
}
}
}
return dp[0][C]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
// Output:
50
|
拿上面程序中的测试用例来看，dp 数组绘制如下，数组的格式也是相同的，不同的就是填充每一个元素时是挑选了可得到的最大值填充的。
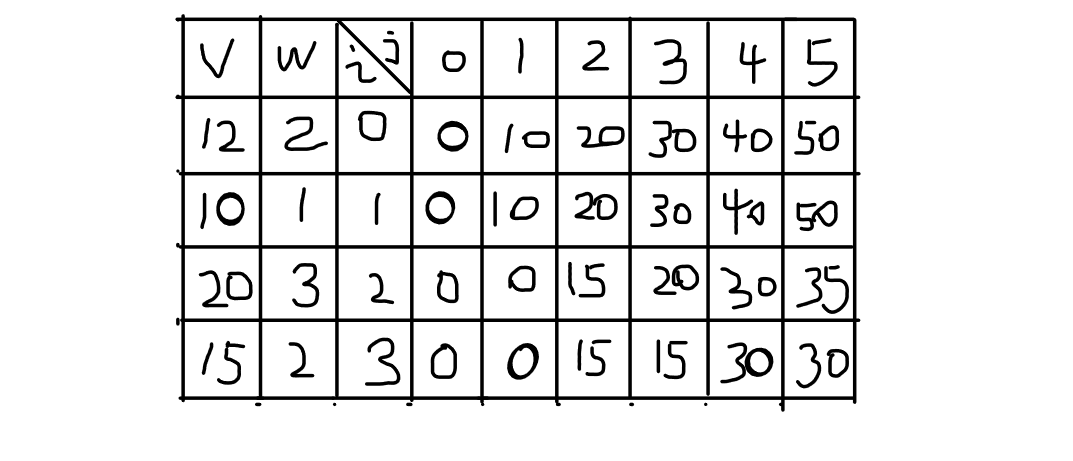
和01背包一样，dp 数组也可以优化为一维数组。
3. 多重背包
多重背包问题是在完全背包的基础上又加了一个条件，那就是每个物品的数量是有限制的，不再是只要背包放得下，就可以无限地往里放。
很容易我们就会发现，解题的程序基本和完全背包没什么区别，只是在填充元素选择最优值时要对物品数量进行判断，不能超过物品数量上限，这里就写程序了。
https://www.cnblogs.com/mfrank/p/10533701.html
支付宝
微信