算法-动态规划

动态规划策略通常用于求解最优化问题。在这类问题中，可能会有许多可行解，每个解对应一个值，我们希望找到具有最优值的那个解，也就是最优解。当题目中涉及「最大」「最小」等词时，很有可能就是这类问题，要考虑是否可用动态规划求解。

1. 基本介绍

动态规划（Dynamic Programming, DP）的思想与分治法很类似，也是把待求解问题分解成若干子问题，不同的是，分治法的子问题是相互独立的，而动态规划的子问题可能重复。我们通过保存已解决的子问题的答案，在需要时就可以直接访问这些已求得的答案，这样可以避免大量重复计算，从而得到多项式时间内的算法。

1.1 找零钱问题

这里拿一个找零钱的问题举例：假设有4分、3分、1分三种硬币面值，要找给顾客6分钱，应该怎么做？我们按以下步骤来思考：

1. 假设要找给顾客的是1分钱，那么只需要一个1分面值的硬币

2. 假设找2分钱，需要两个1分面值的硬币（1分 + 1分）

3. 假设找3分钱，需要一个3分面值的硬币

4. 假设找4分钱，需要一个4分面值的硬币

5. 假设找5分钱，可能是

   • 1 + 4：1个1分面值 + 1个4分面值（硬币数最少）

   • 2 + 3：2个1分面值 + 1个3分面值

6. 假设找6分钱，可能是

   • 1 + 5：1个1分面值 + （1个1分面值 + 1个4分面值）

   • 2 + 4：1个1分面值 + 1个4分面值

   • 3 + 3：1个3分面值 + 1个3分面值

找2分钱的时候重复利用了找1分钱的结果，不过这个不是很明显，最明显的是，找6分钱的时候重复利用了找5分钱的结果（5分钱中 1+4 是最优解法）

1.2 常用概念

动态规划中涉及的一些术语解释如下

对动态规划思想中重叠子问题overlapping subproblem的理解是：前一个阶段的状态可以带当前阶段，当前阶段的状态可以带到下一个阶段，利用表格记录之前所有阶段的状态。放在找零钱问题中，找5分钱得到的状态是 「1个1分 + 1个4分」，这一状态被存起来（通常是一个数组），到下一状态，也就是找6分钱的时候，就可以直接应用这个结果。

从分析中可以看到，我们在每个阶段用的都是上一个阶段的最优解，这就要求我们遇到的问题也必须符合这个性质才能应用动态规划算法。只有原问题的最优解包含子问题的最优解，我们才能自底向上地从子问题的最优解逐步构造出原问题的最优解。

1.3 算法的基本步骤

1. 分析最优解的结构。这一阶段需要我们证明原问题的最优解包含子问题的最优解，运用反证法。首先假设由原问题的最优解导出的子问题的解不是最优的，然后再设法说明在这个假设下可构造出比原问题的最优解更好的解，从而导致矛盾。
2. 递归定义最优值。建立当前阶段最优值和前一阶段最优值的递推关系式，当前阶段的决策为：选中可能解中的最优解。
3. 计算最优值。以自底向上的方式在表格中存储各个阶段的最优值。
4. 构造最优值。从原问题的最优值开始，根据计算各个阶段最优值时得到的信息回溯。

一个容易看懂的步骤为

1. 表示解
2. 表示最优解
3. 根据原问题的最优解和子问题的最优解的关系确定状态转移方程
4. 确定边界条件
5. 利用 dp 数组记录状态，编写程序解决

以最长公共子序列问题为例，使用上述步骤解决，问题描述如下

给定2个序列 $X=\{x_1,x_2,……,x_m\}$ 和 $Y=\{y_1,y_2,……,y_n\}$，找出 X 和 Y 的最长公共子序列。

• 公共子序列只需要保持下标递增的相对顺序即可，元素可以不相邻。例如，序列 $Z=\{B,C,D,B\}$ 是序列 $X=\{A,B,C,B,D,A,B\}$ 的一个子序列，相应的递增下标序列为 $\{2,3,5,7\}$
• 给定2个序列 X 和 Y ，当另一个序列 Z 既是 X 子序列又是 Y 的子序列时，称 Z 是序列 X 和 Y 的公共子序列

分析最优解结构

设序列 $X=\{x_1,x_2,……,x_m\}$ 和 $Y=\{y_1,y_2,……,y_n\}$ 的最长公共子序列为 $Z=\{z_1,z_2,……,z_k\}$。

$X_{m-1}=\{x_1,x_2,……,x_{m-1}\}$;$Y_{n-1}=\{y_1,y_2,……,y_{n-1}\}$;$Z_{k-1}=\{z_1,z_2,……,z_{k-1}\}$

• 若 $x_m = y_n$，则 $z_k = x_m = y_n$，且 $Z_{k-1}$ 是 $X_{m-1}$ 和 $Y_{n-1}$ 的最长公共子序列
• 若 $x_m \neq y_n$，且 $z_k \neq x_m$，则 $Z$ 是 $X_{m-1}$ 和 $Y$ 的最长公共子序列
• 若 $x_m \neq y_n$，且 $z_k \neq y_n$，则 $Z$ 是 $X$ 和 $Y_{n-1}$ 的最长公共子序列

这里假设了最优解，然后分析了三种情况的子问题最优解都包含在原问题的最优解中。

递归定义最优值

定义 $C[i][j]$ 是 $X_i$ 和 $Y_j$ 的最长公共子序列的长度，其中， $X_i=\{x_1,x_2,……,x_i\}$ ， $Y_j=\{y_1,y_2,……,y_j\}$ 。

递归关系为：

存储结构的示意图为

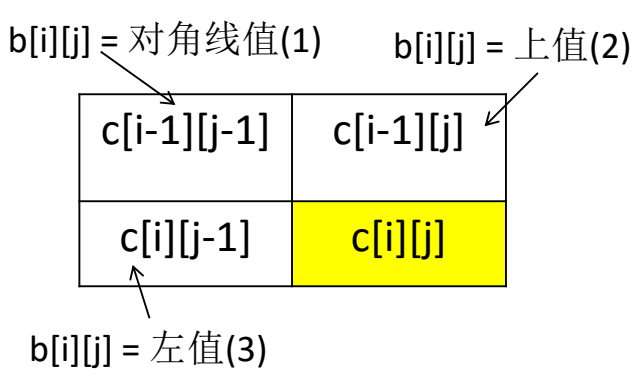
计算最优值

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

LCSLength(x,y,c,b) {
  m = x.length - 1
  n = y.length - 1
  for i = 1 to m do c[i][0] = 0
  for j = 1 to n do c[0][j] = 0
  for i = 1 to m do
	for j = 1 to n do
	  if x[i] = y[j]
		c[i][j] = c[i-1][j-1] + 1
		b[i][j] = 1 // 表示对角线值
	  else if c[i-1][j] >= c[i][j-1]
		c[i][j] = c[i-1][j]
		b[i][j] = 2 // 表示上值
	  else
		c[i][j] = c[i][j-1]
		b[i][j] = 3 // 表示左值
}

构造最优解

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

LCS(i,j,x,b) {
  if i = 0 or j = 0 return
  if b[i][j] = 1
	Lcs(i-1,j-1,x,b)
	print(x[i])
  else if b[i][j] = 2
	Lcs(i-1,j,x,b)
  else 
	Lcs(i,j-1,x,b)
}

结果

设给定的两个序列为 $X={x,y,x,z,y,x,y,z,z,y}$，$Y={x,z,y,z,x,y,z,x,y,z,x,y}$，跟踪算法 LCSLength 和 LCS 的运行结果。为简单计，用 $c[i][j] / b[i][j]$ 表示每个阶段的状态，过程如下

根据 OI Wiki，将 DP 问题主要分为九种，下面进行介绍。

2. 背包 DP

背包问题是最经典的问题之一，普遍出现在动态规划部分和运筹学的书中，下面描述问题

有 n 个物品和一个容量为 W 的背包，每个物品有重量 $w_i$ 和价值 $v_i$ 两种属性，要求选若干物品放入背包使背包中物品的总价值最大且背包中物品的总重量不超过背包的容量。

2.1 0-1 背包

如果选择装入背包的物品时，每种物品 $i$ 只有两种选择：装入或不装入。不能将物品 $i$ 装入背包多次，也不能只装入部分物品。这就是 0-1 背包问题。

形式化问题为：找出一个 n 元 0-1 向量$（x_1,x_2,……,x_n）$ ，使得 $max \sum_{i=1}^n v_i x_i$，需满足以下两个约束条件 $$ \sum_{i=1}^n w_i x_i \leq c \\ x_i \in \{0,1\}, 1 \leq i \leq n $$ 下面证明该问题具有最优子结构性质，即原问题的最优解包含子问题的最优解。

• 原问题：假设当前有 n 种物品，背包载重为 c
• 原问题的最优解：$(y_1,y_2,……,y_n)$
• 子问题：除第一个物品外的 n-1 种物品，背包载重为 $c-w_1y_1$
• 子问题的最优解：$(y_2,……,y_n)$

可以看出，如果原问题和原问题的最优解成立，那么子问题的最优解就成立且包含在原问题的最优解中。

然后来递归定义最优值，通常这个式子也叫做状态转移方程。注意证明过程中给出的最优解的序列先后顺序不一定等于物品的序列顺序。我们定义子问题 $P(i,W)$ 为：在前 i 个物品中挑选总重量不超过 W 的物品，只能挑选一个并使总价值最大，这时的总价值（最优值）记作 $m(i,W)$，其中 $i \leq i \leq n; 1 \leq W \leq C$，得到的状态转移方程如下

如果我们确认了状态转移方程的正确，就不要再想其它的了，不然只会陷入思维陷阱。接下来根据方程编写程序计算最优值与构造最优解即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

Input: n,C, w[],v[]
for W=0 to C do m[0][W] = 0
for i=0 to n do m[i][0] = 0
for i=1 to n
  for W=1 to C
    if w[i] > W
      m[i][W] = m[i-1][W]
    else
      m[i][W] = max{m[i-1][W], v[i]+m[i-1][W-w[i]]}
 return m[n][C]

2.2 完全背包

完全背包问题中一个物品可以选取无数次，而不是一次。子问题的定义与0-1背包相同，但状态转移方程有区别 $$ m(i,W) = max\{m(i-1,W),v_i + m(i,W-w_i)\} $$