算法-分支限界

分支限界和回溯都是有效搜索解空间树的方法，不同的是，分支限界使用广度优先或最小耗费/最大效益优先的方式。

1. 基本思想

首先介绍几个概念

• 活结点：自身已生成但其儿子节点还未全部生成的结点
• 扩展结点：当前正在处理的结点
• 死结点：所有儿子已经生成
• 叶结点：可行解

知道了这几个概念后，分支限界的思想可以描述为：在扩展结点处，先生成其所有儿子结点（分支），在每一个活结点处，估算目标函数的界（限界）。那些导致不可行解或非最优解的儿子结点被舍弃，其余儿子结点被加入活结点表中，然后根据已计算出的函数值，从当前活结点表中选择一个最有利的结点作为扩展结点，使搜索朝着解空间树上有最优解的分支推进。当一个叶结点称为扩展结点时（此时活结点表中其它结点的函数值均不超过该叶结点的函数值），该叶结点相应的解即为问题的最优解。

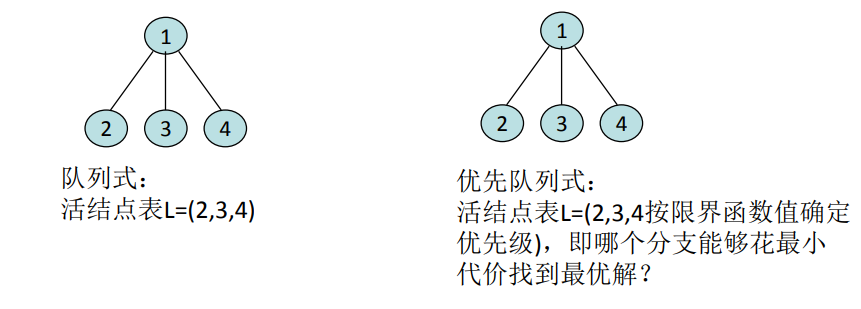
所以可以看出，剪枝的方法和回溯基本相同，不同的是，同一层的所有可行结点组成了一个活结点列表，每次需要在活结点列表中寻找最优的解，实现活结点列表主要有两种方式

• 队列
• 优先队列

2. 旅行旅行商问题

某售货员要到若干城市去推销商品，已知 各城市之间的路程(或旅费)。他要选定一条从驻地出发，经过每个城市一次，最后回到驻地的路线，使总的路程(或总旅费)最小。

旅行商问题的解空间树中，从根结点到任一叶结点就是一条售货员的行走路径，所以我们要做的就是构建这棵树然后找到根结点到叶子结点的最小路径和。

如下，假设有一个在 4 个城市推销商品的例子，构建解空间树如下

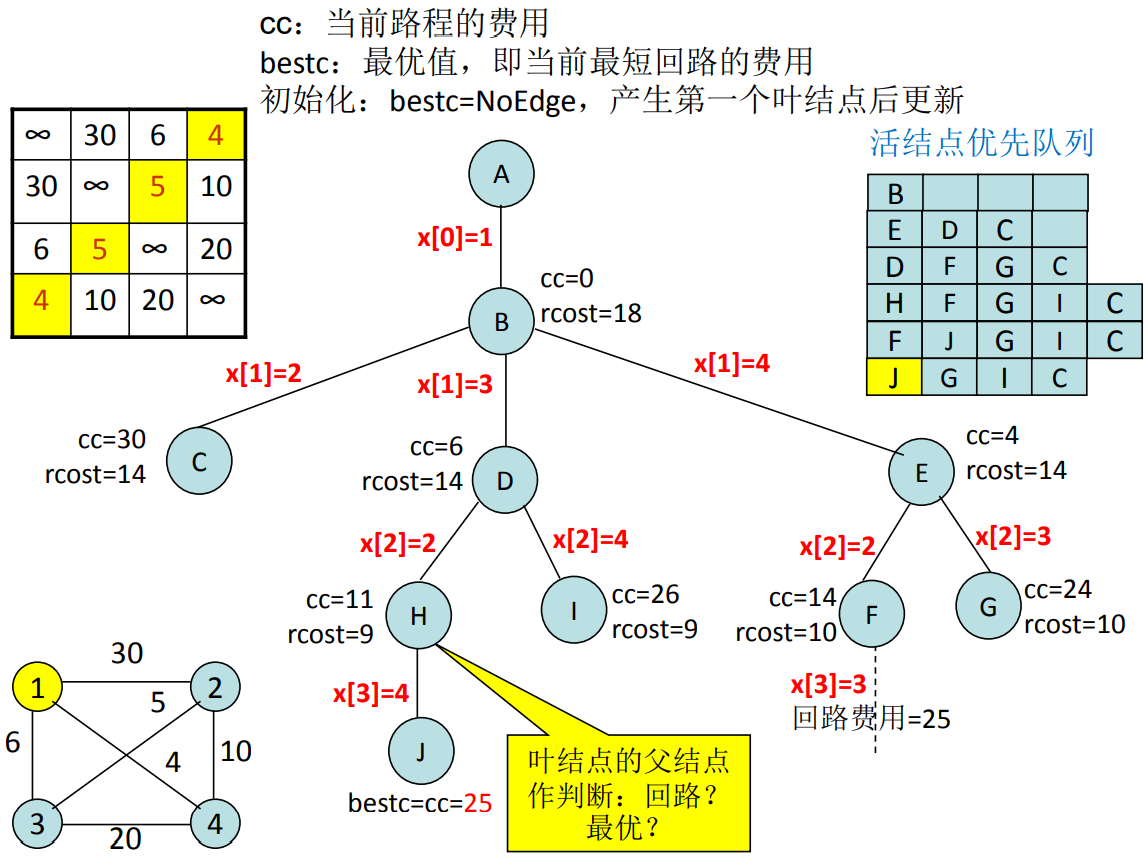
我们选择第 1 个城市作为起点，所以把它加入活结点列表，由于当前只有它一个活结点，将其作为扩展结点。此时当前路程费用为 0 （因为还没开始走），限界函数 rcost 的值为 18，这个数字是这样得到的

• rcost 代表限界函数，其作用应当是找到可行的最优解，这里的最优解就是剩下的路程费用之和最低；
• 剩下的路程费用之和的下界应当这样来计算：所有没有走过的城市相邻边的最小值之和，也就是还没有访问的所有结点的最小出边费用之和，在当前，还位于起点，这就意味着所有的城市都还没走出去，那么四个城市相邻的边的最小值之和就是 rcost = 4(第一个城市) + 5（第2个城市）+ 5（第三个城市）+ 4（第4个城市）= 18
• 我们应当对活结点列表中所有活结点的 cc 值进行比较（cc 是当前路程费用），选择值最小的那个结点作为扩展结点，不过此时活结点列表只有第一个城市，所以只能选择它。

接下来就构建当前扩展结点的儿子结点，遍历所有其它节点，所有与当前扩展结点相邻的城市加入活结点列表，然后计算所有活结点的 cc 值，选择值最小的那一个，这里是第四个城市，以此类推，最终到达叶节点，此时得到了第一个 rcost 值，也就是当前最短回路的费用，其后只要选择 rcost 最小的那个就好。

算法思想可以描述如下

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

//初始化。s：结点在排列树中的层次，cc：当前费用，rcost：x[s:n-1]中顶点,最小出边费用和， bestc：当前最优值
s=0;x[0]=1;x[1:n-1+=(2,3,…,n);cc=0;rcost=Minout*1++Minout*2++…+Minout*n+
bestc=NoEdge
//搜索排列树
While 当前扩展结点非叶结点
	if 当前扩展结点是叶结点的父结点
		if 叶结点存在一条可行回路且该回路的费用小于当前最优值
			bestc = 该回路的费用
			将叶结点插入活结点优先队列（最小堆）
		else 舍弃该扩展结点
	else 产生当前扩展结点的儿子结点
		for i=s+1 to n do
			更新可行儿子结点的状态：cc, rcost
			b = cc + rcost //更新子树的下界
			if b < bestc //子树可能含最优解
				将结点插入活结点优先队列（最小堆）
// 从活结点优先队列中取下一扩展结点

3. 最大团问题

给定一个无向图G=(V,E)。如果U包含于V，且对任 意u,v属于U有(u,v)属于E，则称U是G的一个完全子 图。G的完全子图U是G的一个团当且仅当U不包含 在G的更大的完全子图中。G的最大团是指G中所 含顶点数最多的团。

例如，子集{1,2}是G的一个大小为2的完全子图，但不 是一个团，因为它包含于G的更大的完全子图{1,2,5}中。 {1,2,5}、{1,4,5}和{2,3,5}都是G的最大团。

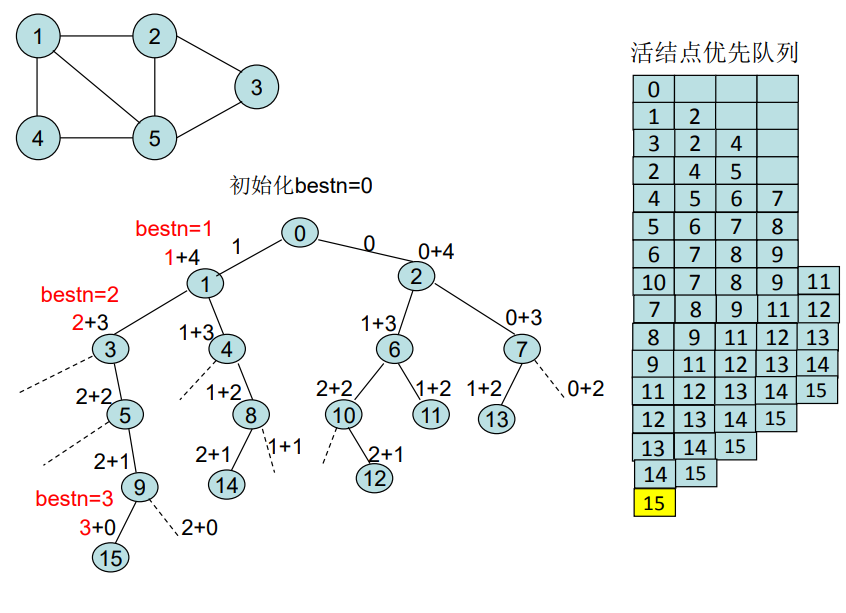
上面的问题其实是图G的顶点集V的子集选取问题，解空间树可以看作一个子集树，剪枝的方法总结如下

• 左子树：从顶点i到已选入的顶点集中每一个顶点都有边， 否则剪枝
• 右子树：顶点数上界小于当前最优值时剪枝，顶点数上界 = 已确定的顶点数 + 未确定的顶点数的上界